이 논문은 딥러닝 기반 추천 시스템인 Neural Collaborative Filtering을 소개한 논문으로 기존의 matrix factorization을 개선한 추천 시스템을 제안했습니다.
Abstract
- 이때 당시 computer vision, natural language processing 등의 분야가 딥러닝을 통해 많은 발전이 이뤄졌는데, 추천 시스템 분야의 collaborative filtering의 문제들을 해결하기 위해 딥러닝을 적용했습니다.
- 기존 collaborative filtering의 문제는 기존에는 user와 item feature간의 interaction을 matrix factorization에 의존하고 latent feature에 inner product를 적용하는 것이었습니다.
- Neural Collaborative filtering에서는 inner product 대신 neural architecture를 이용하였다.
Introduction
Inner product는 user interaction data를 잘 설명하기에는 너무 심플한 linear 연산이므로 neural net을 이용하는 방법을 생각해낸 것이다.
이 논문의 main work는 다음과 같다.
- user와 item의 latent feature를 neural network로 구현하고, 이를 NCF(Neural Collaborative Filtering)라 불리는 general한 프레임워크를 만든다.
- MF(Matrix Factorization)을 multi-layer perceptron으로 높은 수준의 non-linearity를 구현한다.
- 실제 데이터셋으로 NCF의 효과와 전망을 확인한다.
Prelimiaries
이 논문 이전에 발표된 collaborative filtering에 대해 설명하고, 발생한 문제점을 집어보는 섹션이다.
1. Learning from Implicit Data
\(M\) : User \(N\) : Item
\(Y\) : user-item interaction matrix, \(Y \in \mathbb{R}^{M \times N}\)

\(y_{ui}\)가 1일 경우, user와 item i간에 interaction이 있음을 의미하고, 0일 경우 item간에 interaction이 없는(user가 item i를 인지하지 못하고 있는) 상태를 의미하며 item에 대한 선호, 비선호를 나타내지 않는다.
먼저, pointwise loss는 일반적인 머신러닝 패러다임을 따라 objective function(interaction function이라고도 부름)을 최적화하는 방식으로 진행된다. \(y_{ui}\)는 objective function \(f(u, i|\Theta)\)으로 부터 추정되고, 여기서 \(\Theta\)는 model parameter를 나타낸다.
\(\widehat{y_{ui}} = f(u, i|\Theta)\)
objective function은 \(y_{ui}\)와 \(\widehat{y_{ui}}\)의 squared loss를 줄이는 방식으로 최적화한다. negative data가 부족한 경우를 처리하기 위해서 unobserved item을 모두 negative feedback으로 여기거나, unobserved items의 negative instance를 sampling을 하여 얻는다.
두번째로, pairwise loss는 observed entries가 unobserved entries보다 높은 rank를 가져야 하고, observed entry \(y_{ui}\)와 unobserved entry \(y_{uj}\)의 margin을 maximize를 하는 방식이다.
Implicit feedback의 문제점은 Y에서 unobserved item들의 score를 추정하는데 발생한다. (item의 랭킹을 결정짓는 요소이기 때문이다.)
2. Matrix Factorization
MF는 각 user와 item을 latent feature를 실수값의 벡터로 표현한 것이다.
\(P_{u}\), \(P_{i}\)는 각각 user u와 item i의 latent vector를 의미한다. MF는 interaction \(y_{ui}\)를 \(P_{u}\)와 \(P_{i}\)의 내적으로 추정한다.

해당 MF model은 각 latent space가 독립적이고, 일정한 weight으로 linearly 연결되어 있다는 것을 가정한다.
다음 예시에서 내적 연산이 MF를 잘 설명하지 못한다는 사실을 확인해볼 수 있다.

먼저, user와 item을 같은 latent space에서 mapping한다고 할때, similarity는 내적 혹은 cosine similarity로 나타낼 수 있다. 또한, 두 user의 similarity가 유사하게 나왔을 경우, Jaccard similarity로 측정을 하였다.
1-(a)의 그림을 보면 user-item matrix로 구한 user의 유사도는 \(s_{23}\)(0.66) > \(s_{12}\)(0.5) > \(s_{13}\)(0.4)를 확인할 수 있다.
1-(b)의 그림은 \(P_{1}\), \(P_{2}\), \(P_{3}\)를 latent space에 geometric relations를 표현한 것이다.
이제 새로운 user \(u_{4}\)가 들어왔을 때, \(s_{41}\)(0.6) > \(s_{43}\)(0.4) > \(s_{42}\)(0.2)로 \(u_{4}\)는 \(u_{1}\), \(u_{3}\), \(u_{2}\) 순으로 비슷하다는 것을 알 수 있다. 반면 이를 latent space에 표현했을 때, \(P_{4}\)는 \(P_{1}\), \(P_{2}\), \(P_{3}\) 순으로 비슷해 심각한 ranking loss가 발생할 수 있다는 문제점이 발생한다.
위의 예시는 복잡한 user-item interaction을 저차원의 latent space에 내적으로 추정해 발생하는 문제점이다.
이 문제는 latent factor \(K\)를 높이면 해결할 수 있지만 overfitting이 발생한다는 문제점이 발생한다.
Neural Collaborative Filtering
1. General Framework
CF에 neural network를 적용하기 위해, user-item interaction \(y_{ui}\)에 multi-layer 구조를 구현했다.

\({v_{u}^{U}}\), \({v_{u}^{I}}\)는 각각 user u와 item i의 feature vector이다.
- Input layer : one-hot encoding으로 구현된 binary sparse vector를 input으로 이용한다.
- Embedding layer : input layer의 sparse vector를 dense vector representation으로 project한 fully connected layer (이때 만들어진 벡터를 latent factor model의 user (item) latent vector로 생각할 수 있다.)
- Neural CF layers: latent vector를 여러 layer를 거쳐 predicted score를 도출해내는 layer로 마지막 hidden layer X의 dimension이 model의 capability를 결정한다.
- Output layer : \(\widehat{y_{ui}}\)와 \(y_{ui}\)의 pointwise loss를 최소화한다.
NCF's predictive model는 다음과 같다.

이때, user의 latent feature matrix는 \(P \in \mathbb{R}^{M \times K}\), item의 latent feature matrix는 \(Q \in \mathbb{R}^{N \times K}\)이다. \(\Theta_{f}\)는 \(f\)의 모델 파라미터로 \(f\)는 다음과 같이 정의된다.

\(\phi_{out}\), \(\phi_{x}\)는 각각 output layer의 mapping function, x-th filtering layer를 의미한다. 또한, X는 CF layer의 수이다.
model parameter를 학습하기 위해, pointwise method의 squared loss를 사용할 수 있다.
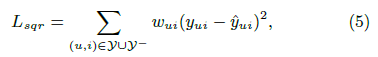
\(y\)는 Y에서 interaction이 observe된 set, \(y{-}\)는 negative instance의 set이다. Predicted score \(\widehat{y_{ui}}\)는 i가 u와 얼마나 연관이 있는지를 나타내며 output layer에서 probabilistic function을 activation function으로 [0, 1]사이의 값을 얻어낼 수 있다. 이를 바탕으로 likelihood function을 정의하면 다음과 같다.

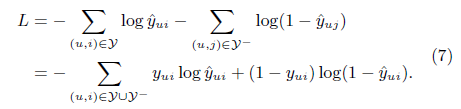
위의 식을 살펴보면, binary cross-entropy loss와 같음을 확인 할 수 있다.
2. Generalized Matrix Factorization (GMF)
여기에서는 NCF framework로 일반적인 MF 얻어낼 수 있다는 것을 확인할 수 있다. user latent vector \(P^{T}v_{v}^{U}\)를 \(p_{u}\)로, item latent vector \(Q^{T}v_{i}^{I}\)를 \(q_{i}\)라고 할 때, 첫 번째 CF layer의 mapping function은 다음과 같다.

output layer를 project한 결과는 다음과 같다.

\(a_{out}\), h는 각각 activation function, weight을 의미한다. 만약, \(a_{out}\)을 identity function으로, h를 1로 이뤄진 uniform vector로 둔다면 기존의 MF model을 완벽하게 복원할 수 있다. 만약 \(a_{out}\)을 non-linear activation function으로 설정해준다면 MF model이 더 expressive해질 수 있다.
3. Fusion of GMF and MLP
NCF framework에서 GMF와 MLP를 합쳐주는 과정에서 각각을 상호보완적으로 강화하기 위해 같은 embedding layer를 사용하는 방법을 떠올릴 수 있다. 하지만 이 방법은 performance를 제한할 수 있다. 따라서 둘을 합친 fused model의 flexibility를 높이기 위해 GMF, MLP 각각 다른 embedding layer를 사용해 따로 학습을 하고 마지막 output layer에서 합쳐주는 방법으로 train한다.


NeuMF model의 objective function은 non-convexity한 특성을 가지고 있기 때문에 저자는 pre-trained model을 사용하는 것을 제안했다. 여기서 한 가지 알아봐야할 것은 마지막 output layer의 GMF와 MLP의 weight을 지정해줄때, hyperparameter를 통해 두 모델의 trade-off를 설정해줘야한다는 점이다.
Conclusion
해당 논문은 기존의 CF의 한계를 deep learning을 통해 해결하고자 했습니다. 다행히도 해당 방법은 CF의 성능을 개선하는데 기여하였고, 모델의 layer를 늘릴 수록 더 좋은 성능을 내었음을 확인할 수 있었습니다. 다음 링크는 논문 저자가 구현한 NeuMF 모델로, 해당 논문을 이해하는데 도움이 될 것 같습니다.
https://github.com/hexiangnan/neural_collaborative_filtering/blob/master/NeuMF.py
GitHub - hexiangnan/neural_collaborative_filtering: Neural Collaborative Filtering
Neural Collaborative Filtering. Contribute to hexiangnan/neural_collaborative_filtering development by creating an account on GitHub.
github.com